Claude Shannon Can Help You Manage Data Flow Scaling in Your Power Grid
The obscure connection between information theory and Bob Newhart.
Claude Shannon laid down the principles of information theory, which is largely concerned with the transmission and reception of information over communication channels. Among the concepts he developed is what is called either Shannon Entropy or information entropy, a concept that deals with the information content in a set of events (such as symbol receptions), using statistical concepts. Figure 1 below shows the basic relationship quantifying information in a discrete set of symbols to their probabilities of occurrence.
The formula in the figure presumes base 2 logarithms, resulting in entropy H having units of bits, which is very useful. Other logarithm bases result in other units: natural logarithms result in units called nats, and base 10 logarithms result in units called hartleys.
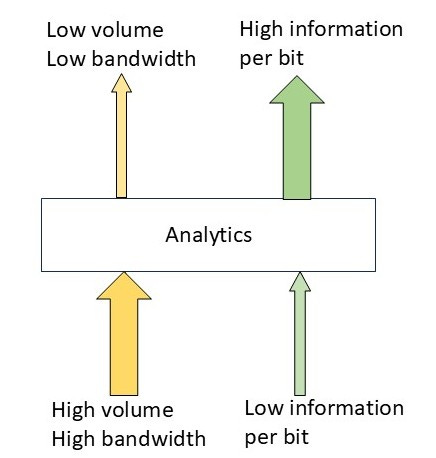
In a previous post, I showed that this formula could be used as the basis for defining analytics, the definition being data transformations that reduce information entropy. The definition can be employed to manage data flow scalability. Figure 2 illustrates this idea graphically.
Analytics, as defined above, can reduce data sets by extracting key information from the original data. For streaming data, the same concept can be applied using information rate instead of information entropy.
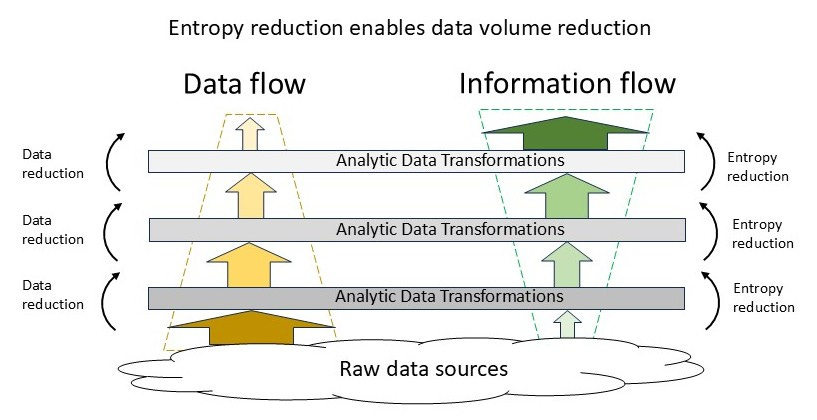
So how does this help manage data scaling? Figure 3 shows a hierarchical set of processes where at each level analytic transformations are used to extract information to pass upward. As we move up the stack, information grows while data volumes or rates decrease.
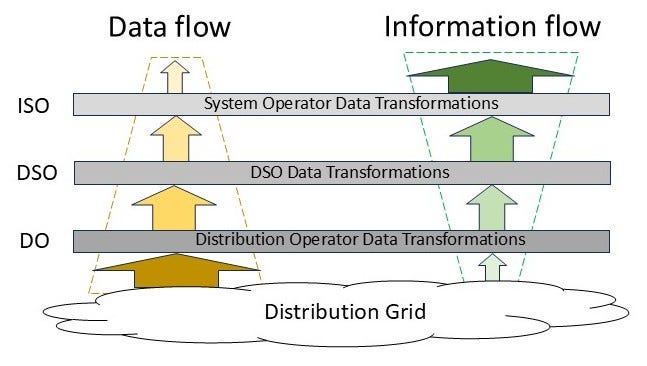
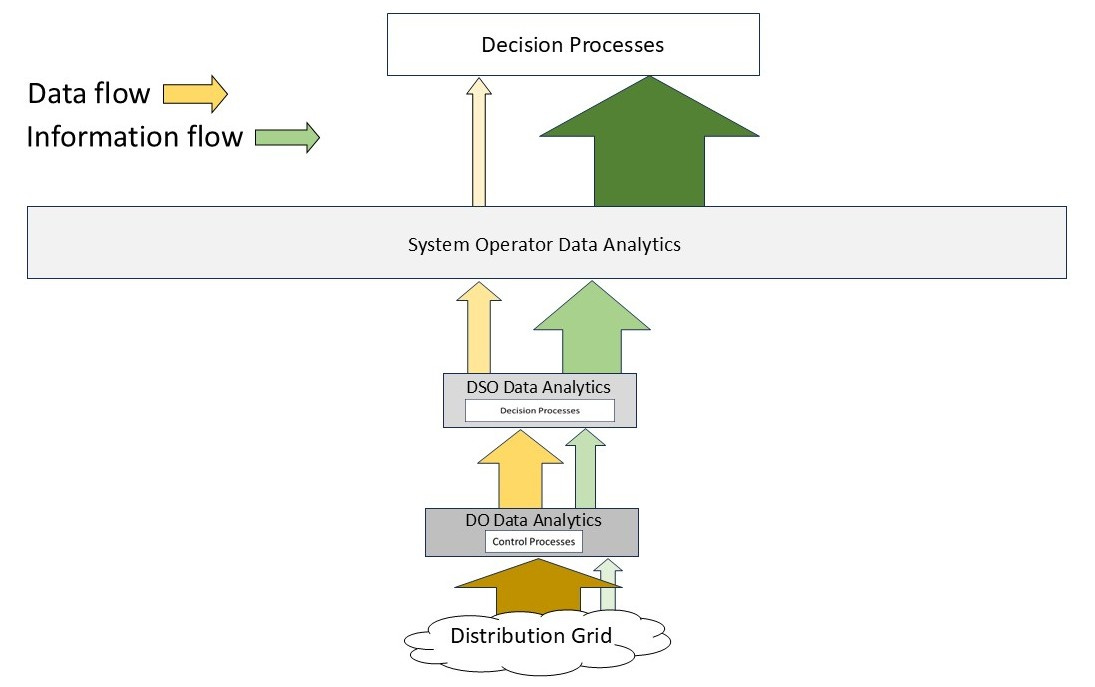
Now let’s map that structure onto a hierarchical model for an electric power system that includes Distribution System Operators (DSOs). Figure 4 shows the mapping in abstract form. For simplicity, it does not show the data/information flows to the system operator from the bulk power system or market participants because we are interested here in the effect of greatly expanding the distribution edge-based resources (some advocates claim this will reach tens to hundreds of millions of devices per regional system).
Figure 5 shows a bit more detail about this structure at the distribution level. Each entity extracts information from its incoming data flow, some for its own use and some to pass upward.
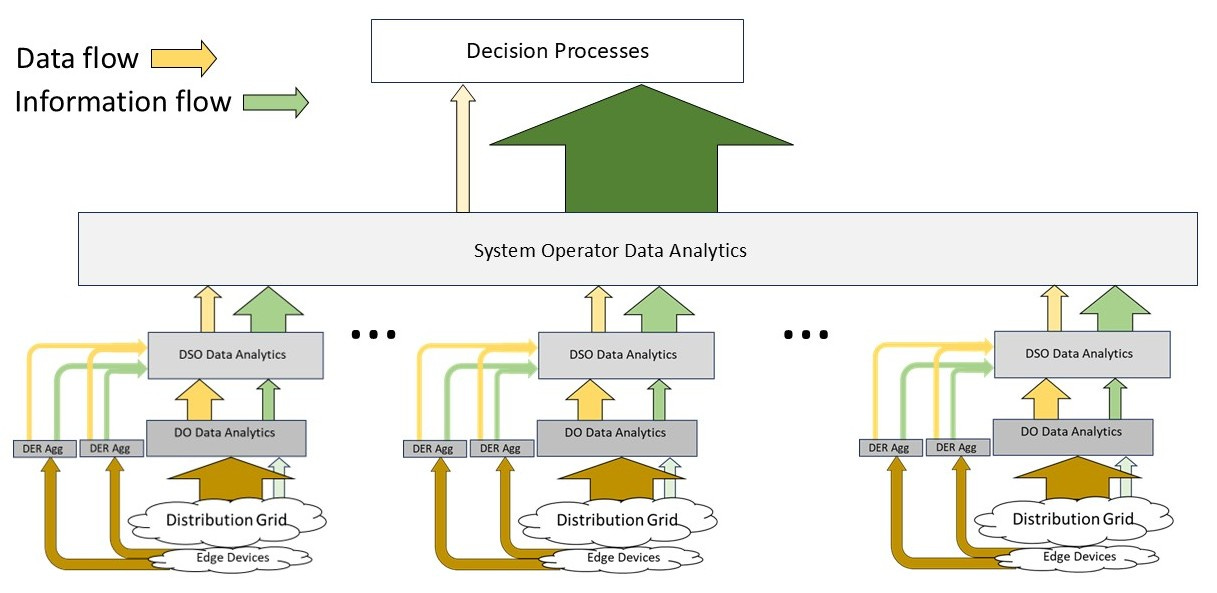
Alas, life is not as simple as that, especially if we are going to have multiple CER/DER1 aggregators. These entities will also produce upward data flows containing information but they too can employ analytic transformations to extract information and reduce data volumes. Figure 6 shows a model where the CER/DER aggregators send their data/information flows to the DSO, bypassing the distribution operators (this is ok provided that the coordination framework, not shown here, is done correctly - a topic for another day).
Of course, regional power systems generally have multiple distribution systems, so the aggregate of all the data/information flows for all the DSOs reaches the system operator. Figure 7 shows why we want to perform entropy reductions using analytic transformations.
Now just step back and imagine if all of the data flows from the distribution level (the brown arrows) were simply merged at the system operator level. At the contemplated scale of CER/DER penetration this would become problematic in multiple ways. The foregoing consideration points to a key role/responsibility that each distribution operator, DSO, and CER/DER aggregator must have: to employ standardized data-reducing analytics as part of an entropy-informed data/information flow structure.
It would be possible to let each distribution operator and CER/DER aggregator provide its analytics outputs to the DSO in unique fashion but then it would be a required role of the DSOs to convert such information as necessary to fit a standard form for transmission to the System Operator (a huge burden on the DSOs). In that case, the set of DSOs would act as a distributed platform to insulate the System Operator from individual distribution operator and aggregator variations. Better to standardize across the board.
So, Claude Shannon’s work on information theory is the basis for a multi-scale information flow architecture that we can use for electric power systems. Boy, somebody should write some kind of Grid Architecture Code for this stuff.
On a side note, Laminar Coordination Framework structure is well suited to to the concept of layered analytics as means to manage data flow scaling.
Customer Energy Resources/Distributed Energy Resources.

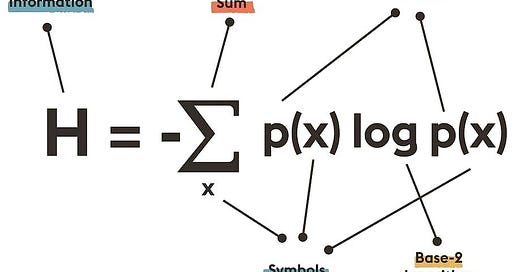





Thanks, Jeffrey. Your posts always make me think. This one was particularly timely as just yesterday I was dealing with the topic of "data" vs. "information'.