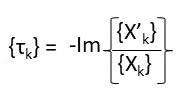Better Way to Calculate Group Delay for Digital Signals - bonus: you get unwrapped phase, too
Sometimes using a more advanced method leads to a simpler solution.
I got interested in finding a good method for calculating group delay for digital filters some time back. The definition of group delay is τ = -dφ/dω, where φ is signal phase and ω is frequency. The usual method for digital signals involves calculating the discrete Fourier transform (DFT) of the filter impulse response or filter coefficient set and then using a simple difference operator on the phase of the DFT. I did not find this to be satisfactory for two related reasons:
calculating phase as tan-1[ Im(X(ω)/Re(X(ω) ] leads to the phase wrapping issue
the phase wrapping issue causes artifacts when a simple difference equation is applied to the phase sequence to get group delay
So I went looking for a way to avoid these limitations by calculating group delay directly from whole signal sequences. I started with the group delay definition, substituted in the inverse tangent formula for phase, and then did the indicated differentiation on digital signals. This led to a slightly messy but usable formula which needed the frequency domain differentiation property of the DFT. That did work, but then I became aware of an approach using homomorphic signal processing, courtesy of a web page by Stanford Emeritus Professor Julius Orion Smith III (see here). Using this more powerful method led to a simpler solution for group delay that gave the same result as my clunkier formula.
The resulting basic formula is:
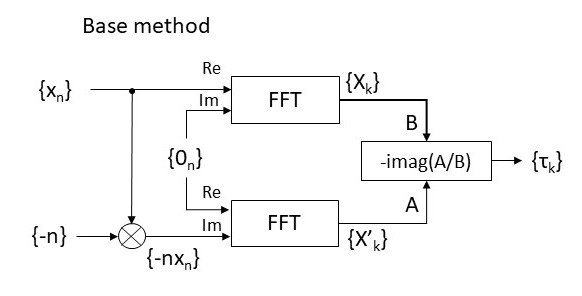
where τk is the group delay, Xk is the DFT of digital signal sequence xn of length N and Im{ } denotes the imaginary component of the complex signal. Note that the solution also uses the frequency derivative X’k which is what leads to the use of the DFT frequency domain differentiation property. The following diagram is a signal flow for the solution (we naturally use Fast Fourier Transforms [FFTs] to calculate the DFTs):
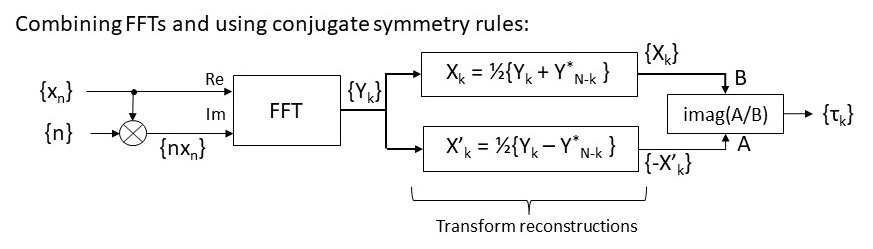
The two minus signs can be removed, but more importantly, we can combine the two FFTs into one by employing the real/imaginary-even/odd conjugate property of DFTs to get:
This method involves less computation than the two-FFT form.
In the conventional method, you calculate phase first, and from that you calculate group delay. But in this new method we get group delay directly, so why not go the other way, meaning integrate the group delay sequence over frequency to get the phase? The phase would be unwrapped because there would be no inverse tangent phase jumps. That signal flow would look like this:
I used the very handy DADIsp signal processing spreadsheet to do a couple of examples using the two-FFT signal flow .
Example 1:
Note that for this well-behaved case, the results are essentially identical.
For the second example, I used an FIR lowpass filter coefficient set:
This time there are significant differences in the results. Note the smooth group delay and phase functions from the new method vs. the ugly functions from the standard approach. Integrating a group delay sequence that has been computed from whole signals avoids artifacts that arise from differentiating phase sequences derived from inverse tangent on individual frequency samples. The standard method uses one FFT, real division, a set of inverse tangent calculations, and differentiation. The new method uses one FFT, conjugate symmetry, complex division, and integration.
Advantage: new method.
Side observation: sometimes using a more advanced method leads to a simpler solution. Here it was homomorphic signal processing vs. differential calculus.